If you have a 100% alpha red circle how many 10% alpha blue circles does it take to completely cover the red circle? The answer is 10, right? No, wait maybe 20? How about 100? Maybe 1,000? Believe it or not, an infinite number of blue circles are required it’s actually impossible. Give it a try in Flash or Photoshop and you will get the following no matter how many times you click:
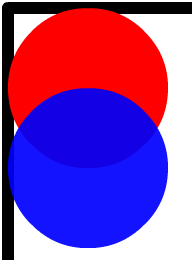
Why?
To busy right now to look for the mathematical explanation to this (but I know there is one!). Adding alpha transparent objects will eventually hit a limit somewhere around 97% rather than reaching one hundred percent. Maybe I’ll take a look later tonight for some additional resources. Anybody know off the top of their head?
Is there any way to get around this?
Add a new layer and stamp a bunch more blue circles. One layer will hit a limit around 97% opacity but two layers each at 97% will appear pretty darn close to 100%, which is expected.
Actually, the 97% limit is just due to your computer’s rounding. Mathematically, it is possible to reach 100% … with an infinite quantity of circles.
http://en.wikipedia.org/wiki/Limit_(mathematics)
Thank you Kulp for your quick response! I had a number of co-workers that believed the full alpha should be reached much sooner (in the 10 to 100 range). The example above has just over 10,000 blue circles overlapped on top of each other.
Actually math implementation of alpha is something like
resultColor = (1-alpha)* backgroundColor+ alpha*foregroundColor
alpha is number between 0 and 1 and transparency of foreground
where function is applied for all R,G,B values of color. so math answer is not 10 it’s infinity.